A la recherche d'une force propulsive
.
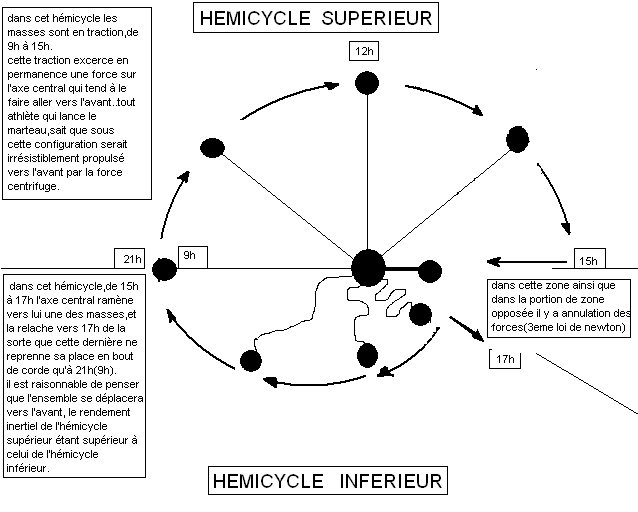
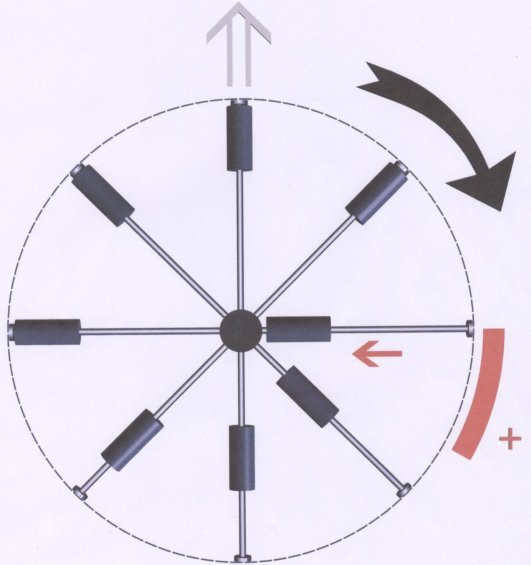
Cette première figure représente un athlète imaginaire capable de faire tournoyer huit marteaux.
Nous traçons autour de lui un cercle virtuel gradué en heures et le sens de rotation des marteaux correspond à celui des aiguilles d'une montre.
L’ épaule gauche correspond à 9h, l’ épaule droite à 15h ; donc,
devant l'athlète (9h, 10h, 11h, 12h, 13h, 14h, 15h).
L'arrière de notre athlète correspond au reste du cadran (15h, 16h, 17h, 18h, 19h, 20h, 21h).
Cette circonférence ainsi créée, notre athlète fait tournoyer ses marteaux de telle sorte qu'entre 15h et 17h, et à leur passage dans cette zone, chacun de ces derniers soit ramené vers sa tête pour être relâché à 17h (nous reviendrons plus tard à cette zone).
A 17h , chaque masse est lâchée pour ne reprendre sa place en bout de corde qu'à 21h ( 9h).
On peut donc constater que dans cette zone là, les masses, avec leur temps de retour en traction, sont totalement indépendantes de l'axe moteur central que constitue l'athlète.
Dans le même temps on peut constater que ce même athlète doit supporter en permanence une traction due au fait que la
zone (9h, 10h, 11h, 12h, 13h, 14h, 15h) est elle, en traction continue.
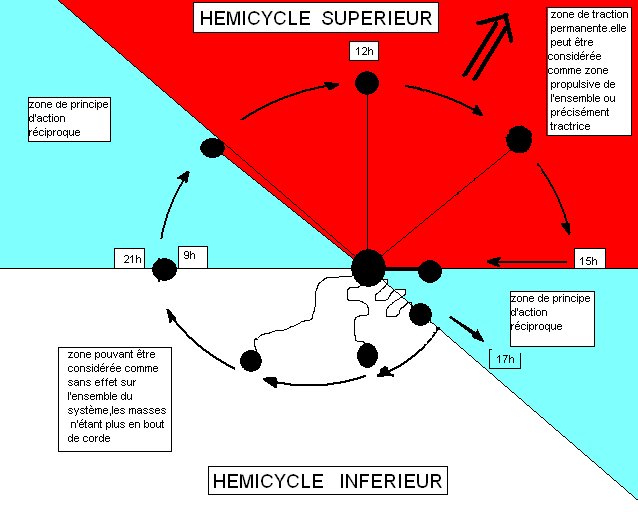
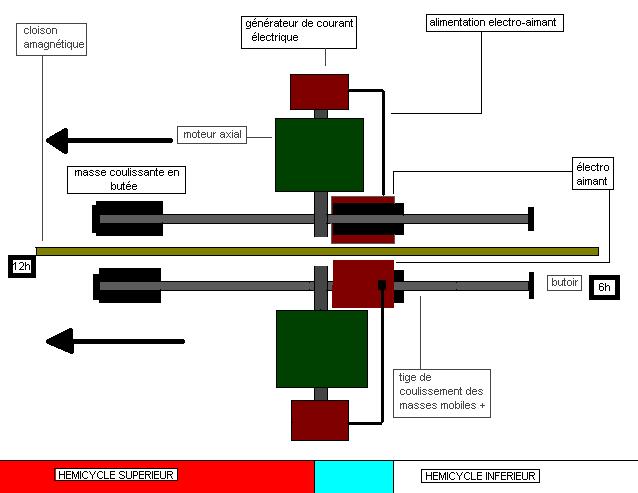
Le déficit de traction dans un hémicycle et le bilan positif de traction dans l'autre hémicycle fait que l'ensemble est propulsé vers l'avant.
Maintenant revenons à la zone 15h 17h.
Il est évident que pour ramener la masse de passage dans la zone vers sa tête l'athlète fournit une force qu'il faut soustraire à l'ensemble ( 3ème loi de Newton); mais que cette zone pour l'exemple a été volontairement
surdimentionnée pour des fins de compréhensibilité.
La technique permet de la réduire et ainsi de pouvoir réduire son effet sur le dispositif.
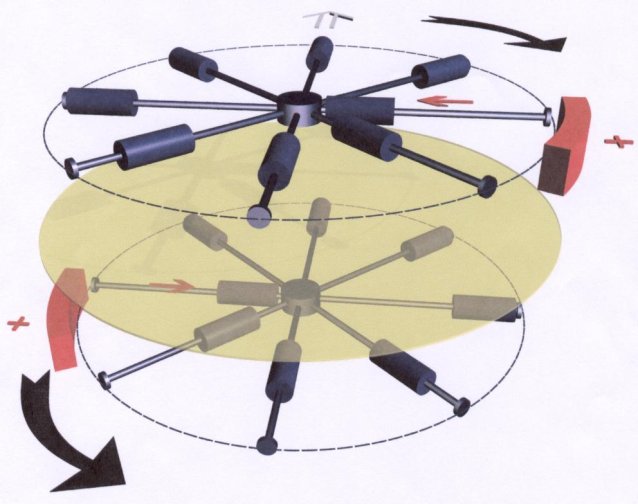
Je tiens toutefois à signaler par avance que l’objet de l'exemple proposé à votre lecture servira de référence en termes de zones, nombre de tiges coulissantes ainsi que principe. |